Chapter 4 Utilities
There are three broad questions we would like to answer in this chapter.
Is there a way for a person to represent how much more one option is preferred to another?
Is there a way to compare one person’s preferences to another that isn’t just the ordering of the options? That is, can we say something more substantial about two people’s first choice, like that one person likes it the most but another dislikes it the least?
How do we interpret what the numbers mean? What are the numbers referring to in the real world? That is, what is their content?
These questions are not just philosophical. There are important practical considerations at stake. For example, the World Health Organization (WHO) has to somehow measure the value of medical interventions. The unit they use in their assessments is called a QALY - quality-adjusted life-year. A QALY incorporates both the quality and quantity of life lived. One QALY amounts to living one year in perfect health, while zero QALY amounts to death. The QALY is not without controversy and the debate ranges from purely philosophical considerations to the deeply pragmatic constraints that policy-makers face.31 Another example that we will look at below is how the concept of utility can motivate arguments concerning social welfare and taxation.
We will introduce the idea of a cardinal utility.32 Supposedly the first use of “cardinal utility” was in 1934 by John Hicks and Roy Allen. The basic idea is to use what’s called an interval scale. In addition to being able to order things using numbers, the numbers are also meant to represent magnitudes. Money is an example of an interval scale, to some approximation. We can use money not only to order things from most expensive to least expensive, but we can also say how much more expensive one thing is to another. One might think, however, that money is ultimately limited in how fine-grained it can be - perhaps it doesn’t make much sense to speak of quantities that are smaller than a cent. Whether or not that’s the case, cardinal utilities can be arbitrarily precise and are typically represented using real numbers (as opposed to whole numbers).33 The “real” in “real numbers” doesn’t mean something like “actual numbers.” The history of numbers and number systems is fascinating (see the Wikipedia entry for “number”). The main thing for our purposes is just to know the difference between integer numbers and real numbers.
If we could build an interval scale for preferences, we might be able to solve some of the limitations of ordinal utilities. For example, suppose there are four books, A, B, C, and D that both Alice and Bob are considering to read together next month. Using just ordinal utilities, it is easy enough for Alice and Bob to order the books with respect to their preferences: each will use 4 to represent their most preferred book, 3 the next preferred, and so on. But remember that we allow for ties, say between B and C. That is, it could be the case that both Alice and Bob agree in their preference orderings, so that \(A\succ B\sim C \succ D\). But what should we make of the situation where Alice assigns 4,3,3,1 for books A, B, C, D, respectively, while Bob on the other hand assigns 4,2,2,1 to them? These numbers preserve the same ordering, and so from an ordinal utility perspective they are the same, but Alice and Bob seem to want to say something different about how B and C compare to the extreme ends of their best and worst options. How do we even go about this?
4.1 Creating an Interval Scale
The Lottery Option Procedure is one way to capture information about how much one option might be preferred to another. Suppose we have just three options and Alice orders them like this: \(A\succ B \succ C\). We want to find how much more Alice prefers B to C, and how much less she prefers B to A. To do so, we create a new option, L. We can think of option L like a lottery that will have A and C as “prizes”. But what should the odds be of winning C in lottery L compared to the odds of winning A? Suppose lottery L has 100 tickets. Given that Alice prefers A over C, it seems that A should be on all of the tickets. But what we want to find out is how B compares to A and C. So what we do is figure out at what point Alice would be indifferent between B and L, where L specifies the fraction of all tickets where A wins and the fraction where C wins. Let’s see some examples to illustrate.
Let’s say lottery L has 50% tickets with A and 50% tickets with C. We ask Alice which of the preferences she has: \(B\succ L\), \(L\succ B\), or \(B\sim L\)?
If Alice says \(B\succ L\), then this means that she prefers getting B to a 50% chance of getting A. That is, she prefers B more than “half as much” as A. But that still doesn’t tell us how much more than “half as much” as A. So, in this case we would change the lottery L to a new lottery L’ by increasing the fraction of tickets that would go to A and then ask for her preference again, comparing B to L’.
If instead Alice had said \(L\succ B\), then that means that she prefers a 50% chance of getting A than getting B. Here we would change the lottery L to a new lottery L’ by decreasing the fraction of tickets for A.
(Indifference) Finally, if instead Alice had said \(B\sim L\), then that means she is indifferent between getting B and a 50% of getting A. Here we wouldn’t have to change anything about the lottery.
Suppose we have gone through this process and we find the lottery where Alice’s preference between B and L is indifferent, i.e. \(B\sim L\). And let’s suppose that L has 75% of the tickets go to A and 25% to C. The idea behind creating an interval scale from this information is to think that Alice’s desirability of B is 75% of whatever her desirability of A is. For example, let’s suppose that Alice’s utility of A is 1 and her utility of C is 0. Then her utility of B would be 0.75. If instead Alice’s utility scale were 0 to 8, with C at 0 and A at 8, then her utility of B would be 6.34 Exercise: draw this as a diagram.
So the introduction of a lottery option helps us make important progress on determining the magnitudes of utilities, but only relative to the utilities of other options. That is, the lottery option procedure doesn’t help us decide what the scale itself should be. It just helps us assign utilities given that we have some scale. To some extent this is a nice feature. Notice that, no matter what scale you pick, the lottery option procedure will always preserve the ordering given by the ordinal utilities, and moreover the resulting cardinal utilities will also preserve transitivity and completeness. We thus have an answer to our first question for how to represent the magnitude that one option is preferred to another.
There are, however, at least two limitations.
First, because the lottery option procedure starts with ordinal utilities, which can only order options relative to one another, it cannot determine an absolute scale, only a relative one. In order to get an absolute scale, we would have to make additional assumptions, like that utilities start at 0 and are maximally 100. But without such additional assumptions, cardinal utilities on the interval scale will be relative to each other.
The second drawback is that it is not possible to do interpersonal comparisons with either ordinal or cardinal utilities, without the aid of additional assumptions. To see this, note the example we had above, where Alice assigns 4,3,3,1 for books A, B, C, D, respectively, while Bob assigns 4,2,2,1 to them. Suppose we do the lottery option procedure on Alice and she is indifferent between B and L, where L has 75% of tickets go to A and 25% of tickets go to D. (Notice since Alice is indifferent between B and C, we could also have used C instead.) Then if Alice’s utilities were cardinal utilities instead of just ordinal utilities, and her scale went from 0 to 4, her preference of B would be 75% of A. Since A has utility 4, then B has utiliy 3. Now suppose we do the same for Bob, and he too accepts the same lottery. Then even though he had assigned 2 to B in his ordering, we know that he prefers B the same as 75% of A. Since A had 4, then as a cardinal utility Bob would give B a 3. However, nothing about this reasoning tells us anything about what the number 4 corresponds to in Alice and Bob. As we had said before regarding ordinal utilities, Alice’s most preferred option might correspond to a great deal of well-being and satisfaction, but that same option might be utterly miserable for Bob, it’s just that the alternatives are even worse. For all we know, Bob’s assignment of 4 is Alice’s assignment of 0. Nothing about the lottery option procedure allows for a comparison between one person’s scale and another’s.
So unfortunately, as far as we have come to this point, the answer to our second question is negative: neither ordinal utilities nor cardinal utilities allow us to make comparisons between people’s preferences beyond their relative orderings. But maybe there are principled ways of making extra assumptions that would help us justify one scale over others, and then combine it with the lottery option procedure so that we can do interpersonal comparisons. In the sections below we will look at some candidate views, which are typically connected to views about well-being or welfare. To spoil things, none of the views except for what is known as the preference-based theory tends to be widely accepted, and even it has limitations.35 There is still a lingering issue that we have not made explicit. Notice that in the lottery option procedure we ask people to have a preference over an expectation. A lottery L is quite a different sort of thing than the options themselves. It asks us to have a preference about a probability that we get an option. This is an important complication we have introduced, and we take it up in the next chapter.
4.2 What do the numbers mean?
4.2.1 Material and money
A naive account of well-being or value might start with material goods. Of course we all need shelter, food, water, and basic commodities to live. But it is widely accepted that material by itself cannot be a good measure of value, let alone utilities. For one, there is far too much diversity between which goods some people find valuable compared to others. I might collect whisky, while someone else collects dolls. If we are going to try to build some interpersonal scale, material goods will be of little help.
Money, on the other hand, can be a very useful guide in approximating the utility of an outcome. It is generally something that we all want, and something we are all willing to give in exchange for the material goods we prefer. Moreover, money also has the feature of putting things in an ordering. If \(A\) has more utility than \(B\), then under some circumstances I’d be willing to pay more for \(A\) than I would for \(B\). That said, there is a massive difference between the idea that money can roughly track utilities and the idea that money and utilities are one and the same. Anyone that thinks money and utilities are identical immediately faces several puzzles.
Here’s one: the more money you have, the less ‘valuable’ an extra $1000 will be to you. Someone that earns $20K a year will find $1K more useful than someone earning $1M a year. Same amount of money ($1K), but different amount of utility.
This is a nice illustration of a more general point about the nature of money. The utility value of $2x is not twice the amount of $x. When you get the first $x, the second $x will be less valuable than the first. Economists call this feature of money declining marginal utility.
Here’s a fictional but illustrative example. Let’s suppose that the increase you get in utility for every extra dollar can be represented by: Utilities = Money\(^{1/2}\). If we plot this function, we get the graph below. Notice that the first few dollars have a sharp rise in utility, but then as we continue to increase the dollar amounts the curve becomes less steep. In other words, the more money you get, the slower the amount of utility grows. The marginal utility is the utility that you get for an extra unit of good (money in this case), and it’s declining because the size of the increase in utility is going down (the precise amount is the slope of the curve at any point, which is the derivative of our function, which is \(\frac{1}{2\text{money}}\)).
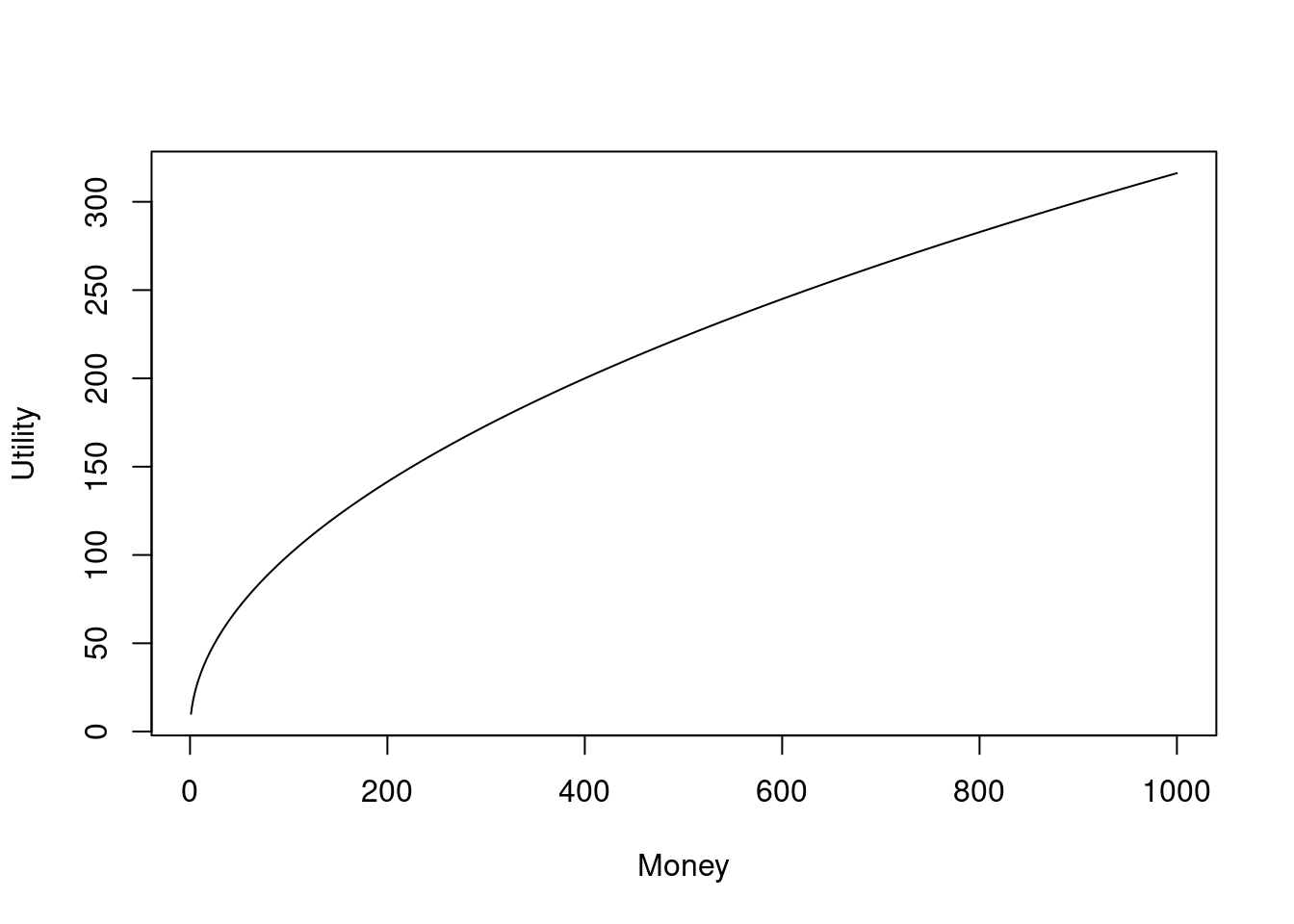 Figure 4.1: Notice that the first 200 dollars get a rise in utilities that’s about 140, but the next 200 dollars (from 200 to 400) only get a rise of about 60 utilities.
Figure 4.1: Notice that the first 200 dollars get a rise in utilities that’s about 140, but the next 200 dollars (from 200 to 400) only get a rise of about 60 utilities.
The fact that marginal utilities decline means that money and utilities don’t have a one-to-one relationship.36 If it were a one-to-one relationship, we would have a straight diagonal line in our plot instead of a curved one. And because money and utilities don’t even have a one-to-one relationship, they can’t be identified as the same thing, even if there seems to be some kind of indirect relationship between them.
This indirect relationship between money and utilities can be used to justify certain taxation policies.37 The history of taxation is a complicated one and the point to be made here is meant to be only illustrative, so we’ll ignore numerous complications. Taxation is a way to help support society at large by funding projects that are beneficial to its members on aggregate (think roads, sewage, public spaces, etc). Except in very special circumstances, here’s a bad way to fund projects: have a flat fee that each person pays each year, regardless of their income. Suppose the flat fee is $1K per year. Superficially, it seems that this is fair, since both the person earning $10,000 (call him Tim) and the person earning $1,000,000 (call her Molly) are contributing the same dollar amounts through taxation. But a utility perspective shows that such taxation is not fair at all. The $1K coming from Tim means he has $9,000 left after taxes, while Molly has $999,000. If we look at their respective loss of utilities from the decreases in their spendable income, Tim is giving up more than Molly. To see this really clearly, imagine someone who only makes $1,000 (or no money at all) - they would have nothing after the flat tax fee (or even be in debt because of it!). Given these kinds of considerations, we can see why there are plausible reasons for taxing the rich “more” than the poor.38 We put `more’ in scare quotes because, while it is more from a monetary perspective, that may not hold from a utility perspective.
The relationship between money and utilities is actually far more curious than what declining marginal utilities suggest. We just saw how getting more money doesn’t lead to an equivalent amount of utility. There are also examples where utility seems to be undermined by the mere introduction of the possibility of representing utilities with money.
For example, suppose a friend asks you for help to move apartments. You consider this to be a favour, one that you expect your friend to return when you move. We can see this as a kind of ‘tit-for-tat’ exchange of utilities: the payoff you get for helping is the promise of getting help in the future (not to mention all the warm fuzzy feelings that come with helping another person generally, let alone just common decency).
But now suppose that your friend offers you one dollar for every hour that you help. From one perspective, that should sound like a great deal: you get all the benefits we just mentioned above, plus an extra two dollars for every hour of your time!
Most people, however, do not see it this way. Once your friend offers you the $2/hr rate, you’re likely to start thinking about what your time is worth in monetary terms, and your friend’s offer is likely to be insulting to you. So, where from a naive perspective we might expect that the offer of money increases your preferences for the outcomes related to helping, it can actually have exactly the opposite effect. Somehow, for whatever reason, the introduction of money, even just the suggestion of it, can be parasitic on utilities related to social norms.
Here’s an interesting twist. Imagine instead of money, your friend offered you beer instead (or whatever your beverage of choice may be). As long as your friend doesn’t mention that the monetary value of the beer is equal to the $2/hr rate, it’s likely that you view the offer as more than fair. But if the beer is playing the role of monetary exchange, then you’d probably ask for more if you think your hourly rate is more than $2.
If your intuitions about this example are in line with this narrative, then it’s consistent with empirical findings concerning favours, gift giving and monetary exchange. (CITE ARIELY) As long as money is not mentioned, social norms dictate some roughly fair exchange of social utilities: I help you knowing that in the future there’s a good chance I can count on you to reciprocate. But once money gets introduced, we tend to switch over to a very different way of thinking about the exchange.
These examples are not meant to suggest that there is no relationship between money and utilities. The point is that, at the very least, there is no straightforward way to substitute between money and utilities. So with that in mind, we turn now to consider what utilities might be.
4.2.2 Hedonism and Experience-based Theories
What makes something good? Or what makes it bad? Jeremy Bentham identified the good with pleasure and the bad with pain. On this view, we tend to avoid painful experiences because pain is identical to badness, and we tend towards good experiences because the good and pleasure are one in the same. This view gives us a neat little picture: someone’s welfare is high if they have lots of good experiences and few bad ones, and welfare decreases as the number of good/pleasurable experiences go down while the number of bad/painful experiences go up.
It doesn’t take long to realize that this picture gets complicated quite quickly. That is, we can find ways in which changes in pleasurable or painful experiences don’t neatly track changes in welfare. For example, earning money can be a painful experience, quite literally if your job involves hard manual labour. And yet at the same time, that person might say that their welfare is going up. They may even say that their welfare is going up because they have to endure some painful experiences.
We might say that’s not quite right. After all, it’s not difficult to imagine that someone might be able to increase their welfare even further if their job were less painful. Then again, if the job were less painful, the pay may go down accordingly. At the very least, what we can say thus far is that there is not some simple relationship between pleasurable/painful experiences and welfare - we can imagine welfare go up even with the introduction of some painful experiences.
There is an argument that, even if we introduce a host of complications, there simply is no account to be given that definitively connects welfare to the level of pain or pleasure of our experiences. The argument comes from a thought experiment from Robert Nozick called the experience machine. Here’s a version of this argument.39 Nozick’s thought experiment was written in 1974, before the movie The Matrix came out in 1999. But if you’ve seen the movie you can easily imagine the sort of scenario that Cypher discusses. We are asked to imagine a matrix-like situation in which a machine provides our brain with all the experiences of a good life - whatever that might mean to you. Like in the matrix, these experiences are not just sensations. The experiences are just like the ones we would have in real life, including the relationships we have with friends and family. The only difference is that the interactions weren’t with real people. But we don’t know that while in the experience machine. To the best of our knowledge, we can’t tell the difference whether our friends and family actually died and they’re just being simulated perfectly, or whether our interactions are with real individuals.
Nozick argues that a person that’s lived a life in the experience machine has lead a bad life. Why? Because their entire world has been based on an illusion. While it is true that the person in the experience machine doesn’t know the difference, if we were to take them out of it, it is likely that they would agree with us that the illusory nature of the experiences they had undermines the level of welfare they would assign to those experiences. If you think that welfare and good experiences track each other perfectly, then you would have to maintain the position that the person living in an experience machine lead a good life.
Notice that the argument isn’t saying that experiences don’t matter to welfare or the good life. Rather, the argument is saying that the character of our experiences is not all there is to a good life. That is, good experiences might be necessary to a good life, but they are not sufficient. What the experience machine argument is supposed to show is that one of the elements that’s missing in an experience-based approach to welfare is the notion of experiences being real.
Even if you don’t find the experience machine argument compelling, there are other issues that remain. My experience of listening to heavy metal may produce pleasure, while it may produce pain in you. The fact that it feels good to me but bad to you suggests that we can’t be having the same experience. If that’s right, then we have to say that there are two different types of experiences being had while you and I listen to the same heavy metal track.
If that’s not right, that is, if there is only one type of experience being had, is there anything that can be said to explain the difference in how you and I perceive the goodness and badness? One attempt might be to distinguish between lower and higher order experiences. That is, we might be having the same lower order experience of the music (this might be something like the `raw’ perception of the music) but we could be having different higher order experiences. I might have a higher order experience of the lower order experience of violent drumming as an expression of existential angst, which feels good to release, while your higher order experience of the drumming might remind you of the frustrations of learning to ride a bike.
There are some good reasons for thinking that our experiences have these multiple levels happening in parallel. The smoker might know very well that they are engaging in risky behaviour, but at the same time that risky behaviour could be providing them with a higher order thrill. That might also be what’s going on for some people when they watch horror movies.
But not all experiences seem to have such multiple levels. When I taste a scotch whisky from Islay (Scotland), I think the the salty, smoky, burnt rubber flavours are good, while many people think those exact same flavours are bad. And this difference doesn’t seem to be one characterized by differences in higher order experiences. That is, our differences in tastes of scotch seem to be just at the lower order. If it’s right, then the challenge for the experienced based view is to resolve the contradiction that the experience is good for one person but bad for another (given that the bad and the good are identified with experiences).
There are additional concerns with the experience-based view concerning the nature of time. A good experience today seems better than the same good experience 10 years in the future. This is not unlike the case of how money works, but it is more general and called discounting the future.
Suffice it to say here that a purely experience-based view doesn’t distinguish between the goodness or badness of an experience relative to your current point in time, and yet we do seem to behave in such a way that the present and near future are somehow different than the distant past or future.
4.2.3 Objective List Theories
Objective list theories start with the recognition that welfare may not be an aggregation of something simple, like a collection of pleasurable experiences. Rather, objective list theories recognize that welfare is a heterogeneous collection of things. We might have something like the following list:
- Good health
- Shelter
- Being in loving relationships with family and friends
- Experiencing beauty
- Engaging in virtuous behavior
- Being rational
- Acquiring knowledge
- Doing things that make a life good, including things on this list
The approach to welfare as a multi-faceted concept is supposedly a strength of objective list theories, but it can also be seen as its primary weakness. There are a few ways to making the objection.
In order for any of the decision making rules to work, they need to assign a number to an outcome. So somehow, the information that’s on a list has to be converted into a single unit of measurement - a utile. A list by itself doesn’t tell us how to aggregate that information. So in order for an objective list theory to work for the decision making rules we’ve considered, it has to also provide such a procedure.
There are reasons for thinking that there is no plausible procedure for converting lists into utilities. For one, the very items on a list don’t seem to be fixed. Different people might have different items on the list (perhaps we should then call it subjective list theory). Or, even if the items on the list are the same, different people might weight the items differently. An academic and an athlete are likely to give different weights to acquiring knowledge and good health. So a procedure for converting lists has to deal with the fact that lists might differ in both the items that are on them and the weights to assign to items.
In order for any procedure to have the capacities just stated, there has to be a way for items on the list to be compared. The main thrust of the objection capitalizes on this requirement and it can be represented in the form of a dilemma.
On the first horn, there is no way of making comparisons between the items such that they can be aggregated into a single number. On this horn objective list theories concede that they can’t provide an account of utilities for the purposes of decision making.
On the second horn, there is a way of making a comparison between the items. Comparisons are only possible if the items have something in common, some way of relating them to one another. But if they have something in common, then why not use whatever that is as a basis for utilities? For example, if the thing in common between experiencing beauty and being in a loving relationship is that they produce pleasurable experiences, then why not just use the experienced-based approach in the first place? On this horn of the dilemma, objective list theories give up the very idea that motivated them in the first place: that welfare is heterogeneous and multi-faceted.
In brief: if welfare is so heterogeneous that the items on the list cannot be compared, then the first horn is faced, but if items can be compared, then the second horn is faced. On either horn, objective list theories aren’t the right account to provide a measure of utility.
4.2.4 Preference-based Theories
One objection common to both objective list theories and experience-based theories is that different people can have different views on what is good for them. That is, what counts as good for me can differ from what counts as good for you. One way to think of this is to say that welfare is something that is subjective, not objective.
Preference-based theories take this kind of objection seriously. On these accounts, what counts as good is that a preference is satisfied. \(A\) is better than \(B\) for an agent if and only if \(A\) is preferred to \(B\) by that agent. If we are talking about some other agent where \(B\) is preferred to \(A\), then for that agent \(B\) is better than \(A\).
Before we consider some complications of this approach, it’s worth noting several advantages. As we already noted, a preference-based theory can handle the issues we raised earlier: that what increases welfare for one person (like our athlete) may not be what increases welfare for another (like our acaedmic).
But another substantial advantage is that preferences can be both nuanced on the one hand, and provide a unifying measure that we can use for utilities. For example, it has no problem handling differences in how people weight different items, or the times at which they would like for the items to be instantiated. For example, one person may prefer a steady stream of somewhat pleasurable experiences, while another enjoys a roller coaster of ups and downs in life. Preference-based theories are sufficiently general to account for such differences.
One serious complication of this view, however, comes from the idea that people could be wrong about what’s good for them. On a purely subjectivist view, whatever a person desires is what’s good for them, and vice versa. It seems perfectly reasonable, however, to say that sometimes people don’t know what’s good for them. Sometimes we think we know what’s good for us, but we’re actually wrong about that. Sometimes our preferences are challenged by other people. Anyone that has had the thoughts, “I wish I didn’t drink so much” or “I wish I didn’t smoke” are good examples of this.
So the trouble is, we want to be able to say both how welfare can be differential across individuals, but at the same time we want to be able to account for the fact that individuals could be wrong about what’s good for them. Surely the right answer is somewhere in between. We don’t expect utilities to be entirely subjective, nor entirely objective. Call this the subjective-objective tension (as opposed to dilemma, which would suggest we have to pick one or the other).
One of the advantages of the preference-based approach is that it needn’t be purely subjectivist. In fact, one of its chief advantages is that we needn’t wait for a resolution in the debate about how to balance the two sides of the subjective-objective tension. All that a preference-based approach demands is that some minimal criteria be met about what preferences are for an individual. Decision theory, as we’re considering it, is about how an individual should decide given their preferences (recall our discussion of instrumental rationality). It thereby sidesteps some of the issues regarding interpersonal comparisons. In the previous chapter we looked at two minimal criteria for preferences (transitivity and completeness) and arguments for them (money pumps).
4.3 Applications and Challenges
Whatever view you might be attracted to about cardinal utilities, let’s have look at an application of them that is not available if we just used ordinal utilities. This is called the minimax regret rule. After examining that rule, we consider some challenges of trying to distill down utilities into a single number.
4.3.1 Minimize Regret
A simple thing we can do with cardinal utilities is give a rough measure of regret. Let’s consider an example. Suppose your options are to party, study, or call your family. Suppose further that tomorrow’s exam will be either very difficult, medium difficult, or easy. Let’s say that you assign the following utilities to the nine possible outcomes.
| Very Difficult | Medium | Easy Exam | |
|---|---|---|---|
| Party! | 1 | 5 | 20 |
| Study! | 15 | 10 | 3 |
| Call Family | 7 | 8 | 9 |
There are different ways of thinking about regret. Here’s one plausible way. Given a particular state, the amount of regret of an option is the difference between the highest outcome among all the options (under the given state) and the option under consideration. For example, under the state Easy Exam, the option to party has the highest outcome. So, the option to party has a regret of 0, the option to study has a regret of 17, and the option to call family has a regret of 11. Using the same strategy, we can calculate the amount of regret for the options under each of the other states. We then get the following table of regrets:
| Very Difficult | Medium | Easy Exam | |
|---|---|---|---|
| Party! | 14 | 5 | 0 |
| Study! | 0 | 0 | 17 |
| Call Family | 8 | 2 | 11 |
Using this regret table, the minimax regret rule says to minimize the maximum possible regret. The strategy proceeds in two steps: first, find the maximum regret for each option (for Party! it’s 14, for Study it’s 17, and for Call Family it’s 11), then second, pick the option with the lowest regret (in our example it’s Call Family).
The minimax regret rule seems intuitive enough. Given the preference assignment, we really prefer to party if the exam is easy, and we really prefer to study if the exam turns out to be very difficult. The option to call family lies somewhere in the middle: no matter how hard the exam turns out, it feels pretty good to get encouragement from talking with family. But we are uncertain about how difficult the exam will be. Because we’re uncertain, and under the assumption that we would rather not regret our choice, our best bet is to call family.
Independence of Irrelevant Alternatives
There is a principle called independence of irrelevant alternatives, or IIA. The basic idea is that if you choose a specific option, like Call Family above, then removing one of the other options shouldn’t change the recommendation. More formally, if option \(x\) is recommended among a set of options \(T\), then if \(S\) is a subset of options from \(T\) and \(x\) is a member of \(S\), then \(x\) should still be the recommended option.
It turns out that the minimax regret rule does not obey IIA. If it did, then that means the option to call family would still be recommended even if we ignored the option to go to the party (maybe it was canceled last minute). But we can show that minimax regret actually changes its recommendation.
To show this, we first take a subset of our previous options and make sure that Call Family is still a member of that subset. We can do this by deleting the option to party from the table above. That gets us this next table.
| Very Difficult | Medium | Easy Exam | |
|---|---|---|---|
| Study! | 15 | 10 | 3 |
| Call Family | 7 | 8 | 9 |
Next we create our new regret table. Notice that this time we’ll get different numbers under the Easy Exam column. This is because the highest outcome is no longer the one where we party and the exam is easy (20) - we’ve removed the party option altogether and thereby the corresponding outcomes. So now the highest outcome under Easy Exam is 9. In the other two columns, the highest outcomes are still the same (they are the study row). When we create the regret table, we then get the following.
| Very Difficult | Medium | Easy Exam | |
|---|---|---|---|
| Study! | 0 | 0 | 6 |
| Call Family | 8 | 2 | 0 |
Following the minimax regret rule, we see that Study has a maximum regret of 6 while calling family has a maximum regret of 8. Picking the minimum of these leads to the recommendation of studying, the opposite of the recommendation it gave when we considered that the party was still on.
If we think that the Independence of Irrelevant Alternatives principle is correct, then that speaks unfavourably to the minimax regret rule. It is not obvious, however, that we should accept IIA. Here are two arguments why we might not accept IIA.
The first argument against IIA comes from empirical considerations. People seem to systematically behave at odds with IIA. A famous example is known as the decoy effect.40 CITE Kahnemann, CITE Ariely Suppose you are deciding between two sandwiches, a small one (say a 6 inch loaf) vs a large (say 12 inch). The small is $6 and the large is $10. Between these two options, let’s suppose that your preference is for the small sandwich - it’s enough to fill you up and costs less than the large sandwich. Now imagine that the store announces a limited time medium sandwich, coming in at 9 inches and $9. A lot of empirical work suggests that your disposition towards the large sandwich changes with the introduction of the medium sandwich, even if you don’t actually have a preference for the medium sandwich. That is, in many cases people will opt for the large sandwich when the medium sandwich is present, but they prefer the small sandwich when it is not, even though the medium sandwich is not preferred. The medium sandwich is called the decoy.
Once you see it, you’ll start noticing the decoy effect in a lot of places, especially in advertising. The effect is not restricted to marketing, however. Its applications are broad, even in dating. Suppose you see Jordan and Taylor at a party and you have a romantic interest in each of them. You find both equally attractive. You know Jordan is a great piano player while Taylor is a great guitar player. You have a bit of a soft spot for piano players, so you’re inclined to strike up a conversation with Jordan (i.e., you have slight preference for Jordan over Taylor). But just as you head in Jordan’s direction, you hear Taylor strumming along to a tune with one of their guitar playing friends, Kennedy. It’s clear that Taylor is a more talented player than Kennedy. Research suggests that because you can compare Taylor to Kennedy - Kennedy is the decoy in this case - your preference can switch from your interest in Jordan to Taylor. Kennedy is irrelevant - you have no romantic interest in Kennedy - but their mere presence can affect your preferences. Of course, you hope that you’re not the decoy for the friend who invited you to the party.41 CITE Dan Ariely
Just because the decoy effect is widespread, however, does not make it a definitive point against IIA. It is possible to say, in IIA’s defense, that people are systematically failing to be rational. How much one takes seriously the empirical data in informing theoretical choices will depend in part on how descriptive and normative aspects of decision theory interact. As a descriptive theory, IIA fails to hold, but as a normative theory we may endorse IIA and point to the decoy effect as a systematic failure on our part to be ideal decision makers (just like some of us systematically fail at parallel parking).
The second argument against IIA, however, comes from theoretical considerations. The thought is that even as part of a normative theory, IIA is too strict of a requirement for rationality. One might think, for example, that when we are considering our options, we should do so holistically. That is, we should not just be comparing options pairwise or side by side until we have a winner. Rather, we should be comparing options as an entire collective. Put differently, when we are considering an option, we should be comparing it to the entire set of alternatives. If that’s right, then even the ideal decision maker would violate IIA.
For example, suppose you collect vinyl records and you’re on vacation somewhere to visit a vinyl shop. You see two records, both of which tend to be difficult to find. Let’s say you prefer record A over record B. As you head to the counter with A in hand, you overhear some people talking about a stash of counterfeits that have been made of A. Such a copy, call it C, is widely available, is also at the store as a kind of gimmick, and it’s noticeably “cheaper looking” than A. So let’s say you prefer A over a copy C, and you also prefer record B to C. To many people it seems perfectly reasonable to think that the popularity of C makes A look less attractive, such that your preferences shift to prefer B over A. After all, B is more unique, seeing as it’s not the sort of thing that there are as many copies of. (Similarly, we might run the story the other way so that instead of there being copies of A, there are lots of copies of B, but this time the fact that there are more copies makes B more special to you because you would have an original.)
We’ll see other theoretical arguments against IIA in more detail when we look at the Allais paradox. To appreciate that argument, we first need to understand the rule for maximizing expected utility, which we’ll cover in the next chapter. The key difference we’ll see between maximizing expected utility and the rules we’ve looked at in this chapter has to do with how they incorporate uncertainty. But first, let’s look at one more application of cardinal utilities.
4.3.2 Multiattribute Approach
In a single-attribute approach, we are forced to make direct comparisons when making decisions. This leads to us making comparisons between things like lives and money: at what point is the dollar cost of a search and rescue too high to save the lives of a few teenagers lost at sea? Here we are placing money and lives and a single utility scale.
In a multi-attribute approach, we allow for there to be multiple scales. Which scales are used depends on the attributes relevant to the decision. In the above example, we might use money to measure the financial costs of a search and rescue, and use number of lives saved as the scale for human welfare. The next step is then to determine how to aggregate the attributes into some overall ranking.
Here’s an example. Suppose a politician is deciding on extending the search and rescue mission for the teenagers lost at sea. There are three attributes under consideration: the cost in dollars for each day of search, the number of lives saved, and the political implications (e.g., getting or losing votes). The politician is considering three options: end search, extend search one week, extend search indefinitely. For simplicity’s sake, we’re going to imagine that there’s only one overarching world state (say, that the teenagers are still alive). For each outcome, the politician could use an ordinal ranking (i.e., a 1 means least preferred, not 1 life saved). Note that even though there is only one world state at the moment (Teens Alive), the outcome for End Search and Teens Alive has three compartments, one for each of the three attributes.
| Money | Lives | Votes | |
|---|---|---|---|
| End Search | 3 | 1 | 1 |
| Extend One Week | 2 | 3 | 2 |
| Extend Indefinitely | 1 | 2 | 3 |
Unfortunately for the politician, there is no dominant option; dominance reasoning will not provide guidance for what to choose. The politician is not limited to the ordinal scale, however. We could instead use an interval (or quantitative) scale. By interpreting the numbers in the above table as cardinal numbers, we can then weight the values of the outcomes with how important each attribute is.
Weighting by additivity
In order to assign weights, we need to assume that they are additive and that the sum of the weights is equal to 1. Let’s suppose that each attribute is equally important as any other. Then since we have three attributes, each one is assigned 1/3. The value of an option for the overarching outcome is then the weighted sum of its subdivided outcomes. For example, the option Extend One Week has a value of \(2\times 1/3 + 3 \times 1/3 + 2 \times 1/3 = 2.333\). Performing the analogous calculations for the other two options reveals that Extend One Week has the maximum value.
| Money (1/3) | Lives (1/3) | Votes (1/3) | Aggregate | |
|---|---|---|---|---|
| End Search | \(3\times \frac{1}{3}\) | 1\(\times \frac{1}{3}\) | 1\(\times \frac{1}{3}\) | =1.667 |
| Extend One Week | \(2\times \frac{1}{3}\) | 3\(\times \frac{1}{3}\) | 2\(\times \frac{1}{3}\) | =2.333 |
| Extend Indefinitely | \(1\times \frac{1}{3}\) | 2\(\times \frac{1}{3}\) | 3\(\times \frac{1}{3}\) | =2.000 |
Suppose instead that Votes is the most important thing for the politician. We might say, for example, that votes are twice as important as lives, and lives in turn are twice as important as money, i.e., Votes are weighted 4/7, Lives at 2/7, and Money at 1/7. Using these weights the Extend One Week option has a (rounded) value of 2.286, but the Extend Indefinitely option has a (rounded) value of 2.429. So different weightings of the attributes can lead to different recommendations.
| Money (1/7) | Lives (2/7) | Votes (4/7) | Aggregate | |
|---|---|---|---|---|
| End Search | \(3\times \frac{1}{7}\) | 1\(\times \frac{2}{7}\) | 1\(\times \frac{4}{7}\) | =1.286 |
| Extend One Week | \(2\times \frac{1}{7}\) | 3\(\times \frac{2}{7}\) | 2\(\times \frac{4}{7}\) | =2.286 |
| Extend Indefinitely | \(1\times \frac{1}{7}\) | 2\(\times \frac{2}{7}\) | 3\(\times \frac{4}{7}\) | =2.429 |
Don’t forget that the columns in this table are all under the state assumption of Teens Alive. You’ll have something similar for the state Not Alive. Later we’ll see how we can combine states and utilities by using probabilities, but that’s in the next chapter.
Non-additive strategy and general challenges
This weighting strategy of the multi-attribute approach assumes that the attributes are additive, i.e., that their relative importance can be summed. Consider again a criticism of the completeness axiom, which can be launched similarly here. The aggregation of attributes on a scale from 0 to 1 that sum in total to 1 is no different than comparing objects on a single scale. It’s the same problem, we’ve just moved from comparison of objects to comparisons of attributes.
Using non-additive criteria is one strategy for sidestepping the above objection while still handling incomplete preference orderings. Suppose each attribute has an aspirational level such that if that minimum level is not achieved, then the corresponding option or alternative is disregarded, even if that option ranks highly in other attributes. For example, suppose that we set the aspirational level for each of the attributes above at 2. Then End Search and Extend Indefinitely will be disregarded because each of them has at least one outcome below 2. Notice that on this strategy the attributes aren’t being compared on some single scale. Each attribute gets to set its own level and then we check to make sure that the options meet that minimum level.
A severe complication of this non-additive strategy is specifying aspirational levels for each attribute: there seems to be both arbitrariness and vagueness to the levels.
There are concerns related to multi-attribute approaches generally. Without some theory for individuating attributes, it is possible that the strategy leads to conflicting recommendations (whether or not they are additive). For example, suppose that a medical products agency is deciding whether to approve a new hand cream. It is unknown whether the long term effects of the hand cream leads to increased toxicity. Toxicity may then be taken as a relevant attribute. Let us suppose that while for half the population the hand cream increases toxicity, for the other half of the population the cream actually leads to a decrease in toxicity. We can suppose that whether it does or doesn’t depends on something genetic. If we conceive of toxicity as a single attribute, then the average increase in toxicity is zero because one half of the population cancels out the other. By these lights, the hand cream might get approved. It seems reasonable, however, to characterize toxicity in terms of two attributes: “toxicity for people with gene A” and “toxicity for people with gene B”. If we individuate attributes in this way, the recommendation may be to not approve the hand cream if the risk for people with one of the genes is sufficiently large. So here is an example where there are two different ways of aggregating risks that lead to conflicting recommendations, and since we have no way of determining which is the correct way of individuating attributes, a multi-attribute approach does not solve the problem of dealing with incomplete preference orderings.
4.4 More Challenges and Final Remarks
There is much more to be said about the notion of utilities. Even in the more minimal case of preference-based theories, we assume that they are transitive and complete. Moreover, we have implicitly assumed that a person knows what their own preferences are, at least in the moment. But there are good reasons for thinking that in many scenarios we don’t know our own preferences and look towards others to either discover or create our own. We also have reasons for thinking that preferences can change over time, and in some cases it seems that the way our preferences change is not predictable beforehand.
Even if individuals had unchanging preferences that they knew perfectly, there are good reasons for treating utilities across time differently. It seems plausible to think that a unit of utility is more valuable today (from your perspective on the present day) than it is ten years from now. After all, there’s no guarantee that you’ll live another ten years to obtain that unit of utility, and it’s far more likely that you’ll live through today. Investing money illustrates a similar idea quite nicely. $1,000 dollars today is worth more than $1,000 next year (even if we increase this amount to account for inflation) because you can invest it today and turn it into more than $1,000 by next year (market crashes notwithstanding). For these sorts of considerations, we often discount our future selves in the decisions we are making in the present. That is, while it is important to think about yourself in the future, the preferences of your future self should not be given the same weight as you in the present. Again, who knows if your future self even comes to be: as the famous economist Maynard Keynes said, “In the end we are all dead.”
Interesting, it’s not clear whether we should apply the same sort of thinking when we are considering decisions at the aggregate or group level. Unlike the guarantee that your life will come to an end and we have a decent sense of how long you will not live, the life of communities is far more open-ended. In fact, society is likely to go on far longer than individuals that it makes sense to model society as if it were to go on forever - this is sometimes referred to as the ‘infinite life’ assumption in economics. Without an endpoint in sight, it’s not clear how much we should be discounting future generations. In fact, some philosophers and economists suggest that, given that we have some moral obligations to future society, we shouldn’t discount future generations at all. Frank Ramsey said, “In time the world will cool and everything will die, but that is a long time off still, and its present value at compound discount is almost nothing.” So while the death of individuals warrants the application of a discount function, the death of society is so far off that the "same’’ reason does not apply here. Once again we see there is a kind of discontinuity between decision making at the level of individuals and the level of groups.
All of these considerations raise interesting questions about how preferences affect decision making. But we need to return to the idea of an expectation in the first place. To do that, it is not enough to just think in terms of utilities. We have to be more explicit about the notion of a probability, like we used in lottery option procedure, and how they are used in models of decision making. We turn to that next.
Exercises
Suppose we have a utility scale that goes from 0 to 5 and we’re trying to determine what utility Alice assigns to an option called \(D\). We know that Alice has the preference ordering of \(A\succ D \succ C\). Suppose we present Alice with a lottery option \(L\) and we determine that Alice said \(D \sim L\) when \(L\) consists of 60 tickets of \(A\) and 40 tickets of \(C\).
- What utility does \(D\) have for Alice assuming that \(A\) is 5 and \(C\) is 0?
- What if instead \(A\) is 4 and \(C\) is 3?
Which interpretation of cardinal utilities (hedonism, objective list theory, or preference-based) do you find most compelling? Why?
Provide an application of the minimax regret rule to one of your own decisions. Remember you will need two tables, one is the standard utility table, the second is the table of regrets (which you calculate from the utility table).
- Does the recommendation of the minimax regret rule correspond with your intuition about what to do?
- Does your example obey the principle of independence of irrelevant alternatives?
Provide an application of the multiattribute approach to one of your own decisions, using weighting by additivity.
- Does the recommendation of the multiattribute approach correspond with your intuition about what to do?
- If not, is there any way to update the weights so that it would?
- If so, how much could you change the weights so that the approach would make a different recommendation?